Io sono in ferie. Nel senso che sto tentando di tenermi lontano dal 'puter per qualche giorno, disintossicarmi. E cosa si fa in questi casi? Altro, per esempio rileggere i classici. Io sono alle prese con Gödel, Escher, Bach di Douglas Hofstadter (1979, versione italiana 1984).
Sì, ho copiato da me, l'altro blog, quello noioso. Ma è perché questa notte nel cap. VIII, L'Aritmetica Tipografica ho trovato una cosa che vi devo davvero raccontare. Copio (p.241-2):
Manca qualcosa
Se ci si mette a sperimentare per un po' con le regole e gli assiomi dell'AT finora presentati, si troverà che si può produrre la seguente famiglia piramidale di teoremi (un insieme di stringhe che provengono tutte da uno stesso stampo e che differiscono tra loro solo per il fatto che vi sono stati inseriti i numerali 0, S0, SS0 e così via):
Si dà il caso che ognuno dei teoremi di questa famiglia può essere derivato da quello che lo precede immediatamente con solo un paio di passaggi. Si tratta perciò di una specie di "cascata" di teoremi, dove ogni elemento innesca il successivo. (Questi teoremi assomigliano molto a quei teoremi del sistema pg in cui le stringhe di trattini posti al centro e sulla destra crescevano simultaneamente).
Orbene, esiste una stringa che possiamo scrivere facilmente e che riassume il significato passivo di tutti questi teoremi nel loro insieme. Tale stringa-riassunto fa intervenire un quantificatore universale, eccola:
Eppure con le regole date finora non si riesce a produrla. Ci provi il lettore incredulo!Solo un paio di delucidazioni. Seguendo Peano 0 sta per 0, zero; S per successore, quindi S0 è il numerale 1, SS0 il 2 e così via. La stringa-riassunto si può leggere come "per ogni numerale a si ha che 0 + a è uguale ad a". Il modo M (meccanico) differisce dal modo I (intelligente) in modo (ahemmm) che qui do per scontato, intuitivo.
Viene fatto di pensare che si potrebbe trovare immediatamente un rimedio alla situazione adottando la seguente
Regola della totalità (proposta): Se tutte le stringhe di una famiglia piramidale sono teoremi, allora la stringa universalmente quantificata che le riassume tutte è ancora un teorema.La difficoltà che si ha con questa regola è che non è possibile applicarla nel mondo M. Solo chi riflette sul sistema può sapere che tutte le stringhe di un insieme infinito sono teoremi. Questa regola non si può perciò incorporare in un sistema formale.
Uepp! verrebbe da dire, anzi lo dico proprio chiaro e forte, nèh!
E ho un testimone, anzi una testimone eccezionale: Alice. Ecco la sua testimonianza, presa da qui:
— Voi, signore, sembrate abilissimo nello spiegare le parole, — disse Alice. — Mi fareste la cortesia di dirmi il significato della poesia intitolata Giabervocco?Ecco, Alice ha capito ed è uscita dal sistema! Proprio come ho fatto io con il GEB. È talmente naturale che manco te n'accorgi; e lo fai continuamente (anche se la parola "meta" la sanno solo i saputi (e io che la uso ogni tanto, ma senza abusarne)).
— Sentiamola, — disse Unto Dunto. — Io posso spiegare tutte le poesie che sono state scritte... e molte che non sono state scritte ancora.
Questo sonava molto attraente, e Alice ripetè la prima strofa:
S'era a cocce e i ligli tarri— Basta per cominciare, — interruppe Unto Dunto: — qui vi sono molte parole difficili.
girtrellavan nel pischetto,
tutti losci i cincinarri
suffuggiavan longe stetto.
“Cocce” significa le dieci della mattina, l'ora in cui si comincia a cuocere i cibi per la colazione.
— Bene, — disse Alice, — e “ligli”?
— Ligli significa agile e limaccioso. “Li” è lo stesso che “attivo”. Due significati in una parola sola.
— Ora comprendo, — osservò Alice pensosa, — e che sono i “tarri?”
— “Tarri” sono degli esseri simili ai tassi... alle lucertole... e ai cavaturaccioli.
— Che creature strane che debbono essere!
— Sì, — disse Unto Dunto, — e fanno i nidi sotto le meridiane e vivono di formaggio.
— E che vuol dire “girtrellare”?
— Girtrellare vuol dire rotare come un giroscopio e far buchi come un trapano.
— E il pischetto?
— La zolla d'erba intorno alla meridiana. È detta pischetto perchè si espande un po' innanzi e un po' dietro la meridiana...
— E un po' da ogni lato, — aggiunse Alice.
Però, controesempio, molto autorevole anche lui, Neander. Non so se vi ricordate le Interviste Impossibili che la Rai trasmetteva quando ero giovane, ecco Italo Calvino che intervista l'Uomo di Neanderthal. È divisa in tre parti, la testimonianza in oggetto inizia al sesto minuto della seconda parte e raggiunge il climax a 0:30-1:15 della terza parte:
Chiaro no? E, in ogni caso, niente panico: posso smettere quando voglio. Volendo.


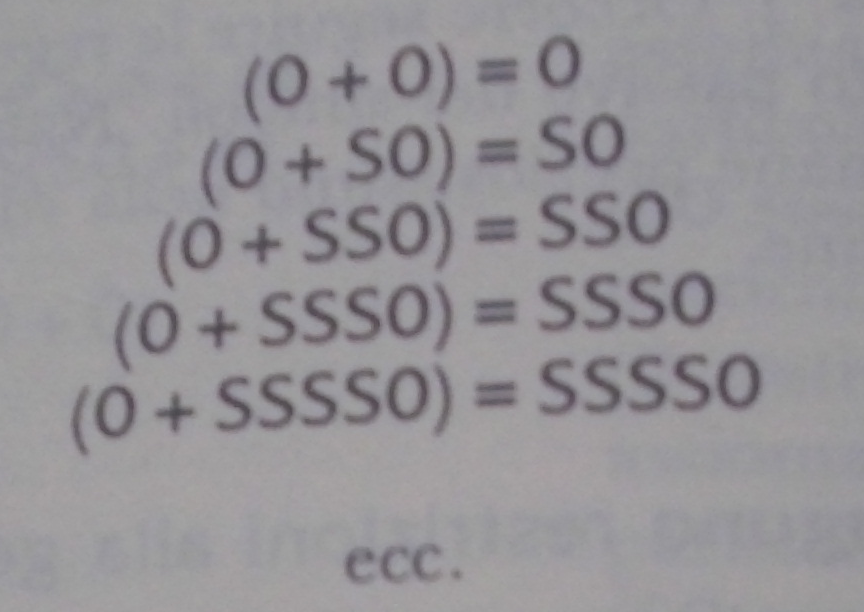

Nessun commento:
Posta un commento